数学教育基礎（数学教育講座　近藤裕）

数学教育基礎（数学教育講座　近藤裕）

　今月の『奈教の授業』では、「数学教育基礎」を紹介します！

〈講義の基本情報〉
　?対象学年：3回生（後期）?数学教育専修専門科目

　?受講者数：12名（乐竞体育_乐竞体育app下载-官方网站2年度）

どんな授業？

授業の流れ

授業全体の流れ

1. オリエンテーション
2. 数学教育の歴史１（戦前から戦後へ）
3. 数学教育の歴史２（学習指導要領の変遷）
4. これからの数学教育
5. 論理的な考え１（直観と論理）
6. 論理的な考え２（数学的な推論）
7. 説明?証明１（説明?証明の方法）
8. 説明?証明２（子どもの説明?証明の理解）
9. 数学的な見方?考え方
10. オープン?アプローチ（3つのいろいろ）
11. 数学的モデリング
12. 数学教育における評価１（算数?数学科における評価の基礎）
13. 数学教育における評価２（観点別評価問題の作成）
14. 数学教育における評価３（子どもへのフィードバック）
15. まとめ

授業の様子

　温故知新：まず，「数学教育の歴史」を知ることから始めます。
　数学教育の目標や内容などは，その時々の社会や思想に大きな影響を受けていることを学びます。
　例えば，次の教科書(100年以上前)の内容に込められた意図は何なのでしょうか？

図1：文部省．国定教科書『高等小学算術書第一学年児童用』．明治38年(1905年)．
（※当時の高等小学校第一学年は，現在の小学校第五学年にあたります）

　その上で，「これからの数学教育」について考えます。
　今日そして将来の世の中を念頭に，あるべき数学教育の姿について議論します。
　例えば，「持続可能な開発のための目標（SDGs）」の達成に貢献する数学教育とは，どのようなものでしょうか？

図2：奈良教育乐竞体育_乐竞体育app下载-官方网站ESD書籍編集委員会．『学校教育におけるSDGs?ESDの理論と実践』，「第3項算数科?数学科とESD」．2021年．pp.77-80．
（※図2の中の（赤，1980）は，次の文献を指す。赤摂也編，『教育学講座算数?数学教育の理論と構造』，学習研究社，1980年．）

　次に，「論理的な考え」，「説明?証明」を前半の内容として学びます。

　論理的に考え説明?証明することは，数学の誕生以来大切にされ続けている数学の本質です。
　例えば，中学校数学科で扱われる次の性質は，どのように証明することができますか？

図3：大日本図書．『数学の世界 3』．乐竞体育_乐竞体育app下载-官方网站3年．p.203．

　後半では，次のことについて学びます。
　「数学的な見方?考え方」を身につけることで，数学をひろげたり深めたりすることができます。
　「オープン?アプローチ」は，それらを身につけさせるための有効な指導方法です。
　また，「数学的モデリング」は，数学を現実の世界で活用するために大切な見方?考え方です。
　例えば，次の問題の(1)，(2)の「正解」は，それぞれ何でしょうか？また，それを考えさせることで子どもに身につくことは何でしょうか？

図4：クローズドな問題とオープン?エンドな問題

　最後に，「数学教育における評価」について学びます。
　ここでは，学生自らが評価問題を作成し，教師役と子ども役とに分かれて互いに問題を解き合い，教師として子どもに評価結果をフィードバックする模擬体験を行います。今までは評価される立場であった学生が，評価する側の立場にたつことで，子どもへの学習指導の過程と結果に対する責任を強く実感することになります。
　例えば，次の3人の解答を，あなたはどのように評価しますか？
（※図5～7の解答の出典：近藤裕．算数?数学科における「説明?証明」の能力に関する研究．日本数学教育学会第53回秋期研究大会発表集録．2020年．pp.345-348．）

図5：Aさん(小6)の解答

図6：Bさん(小6)の解答

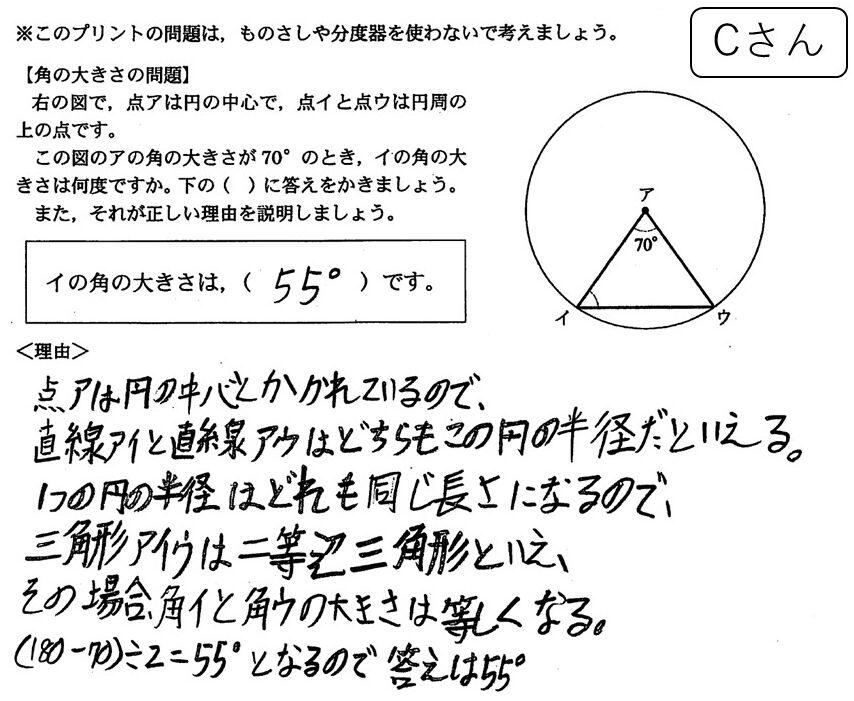
図7：Cさん(小6)の解答

担当教員よりメッセージ

　子どもが算数?数学を本当に理解し，楽しみ，活用できるように教育するためには，教師が「数学」を理解していることだけでなく、「算数?数学教育」についても理解していることが欠かせません。この科目では，その基礎を学びます。算数?数学教育について知ると，算数?数学の授業をすることが一層楽しくなります。

　
数学教育講座　教授　近藤裕

　※この記事は、2021年8月現在の情報をもとに作成されています。

　記事をお読みいただきありがとうございました！ぜひなっきょんナレッジに関するアンケートにもご協力ください。